本文主要对平面凸包的计算的学习
问题描述
凸:如果平面的一个子集S被称为是“凸”的,当且仅当对于任意两点p, q ∈ S,线段 pq 都完全属于S,集合S的凸包CH(S),;
问题描述:在平面中给出N个点,找出一个由其中某些点作为顶点组成的凸多边形,恰好能围住所有的N个点。
给定平面点集 P = { p1, …, pn },通过计算从 P 中选出若干点,它们沿顺时针方向依次对应于 CH(P)的各个顶点。
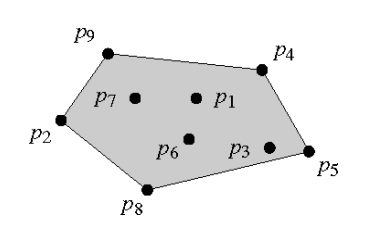
input = 平面上一组点:p1, p2, p3, p4, p5, p6, p7, p8, p9
output = 凸包的表示:p4, p5, p8, p2, p9
主要的算法
主要的算法有:
- 极点法
- 极边法
- Jarvis March
- Graham Scan
Graham Scan Algorithm
时间复杂度为O(nlgn)
数学知识回顾
两个向量的叉乘p1Xp2:
- |向量c|=|向量a×向量b|=|a||b|sin
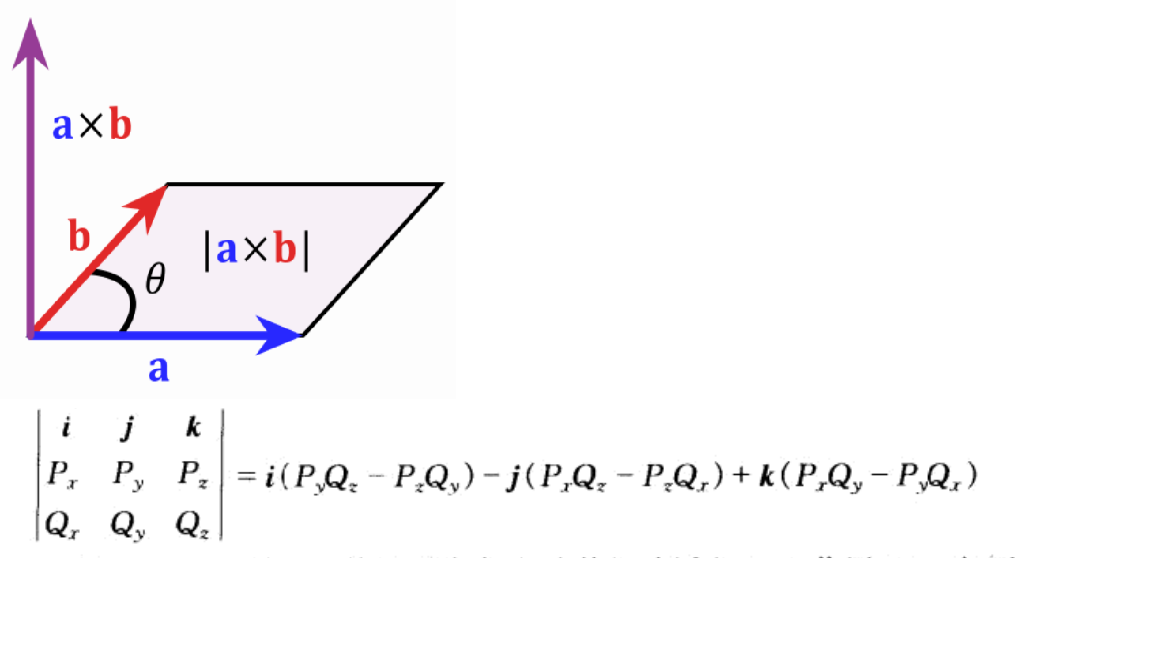
- 可表示平行四边形的面积,
- 二维向量看作成z轴值恒为0的三维向量,例如向量OP1(x1,y1,0),OP2(x2,y2,0),
OP1 x OP2 = (0,0,x1y2-x2y1,很明显(0,0,x1y2-x2y1)也是一个向量,并且是垂直于向量Op1和Op2构成的平面的法向量,
而其方向的正负就取决于它们的输入(x1,y1)和(x2,y2)的值。
- 如果小于零则说明p1在p2的逆时针方向。
- 如果大于零则说明 p1在p2的顺时针方向。
- 等于0 则共线.
- p1Xp2 = - p2Xp1
- 可用于判断一个点是否在一条线段的左边还是右边
- 可用于判断两条线段是否相交.
例子:判断两线段AB 和CD 是否有交点。同时满足两个条件:
- C D分别在AB两侧(AB X AC) *(AB X AD) <=0
- A,B分别在CD 两侧 (CD X CA) *(CD X CB) <= 0
伪代码

算法理解和实现
1.在平面输入的点集中,首先 找到这些点中处于最下方的点,如果y值相等则找最左边的点.假设该点为p0.
int k=1;
for(int i=2;i<=N;i++)
{
if(p[i].y<p[k].y||(p[k].y==p[i].y&&p[i].x<p[k].x))
k=i;
}
swap(p[1],p[k]);
2.把输入几何以上述的p0点为极点并按照极角(polar angle)从小到大排序,极角相同的点按照到极点的距离从小到大排序。
//计算叉积,小于0说明p1在p2的逆时针方向(右边),即p0p1的极角大于p0p2的极角
// p0p1 x p0p2
// 以为我们觉得叉积是一个向量,而不是一个标量,这里仅仅返回叉积的三维度的结果,从来到判断两个向量的位置关系问题.
// 如果小于0;p2在p1的右边
//
double cross_product(Point p0, Point p1, Point p2)
{
return (p1.x - p0.x)*(p2.y - p0.y) - (p2.x - p0.x)*(p1.y - p0.y);
}
bool compare(const Point &p1, const Point &p2)
{
double temp = cross_product(p[0], p1, p2);// 可参考第二小节数学知识回顾
if (fabs(temp) =0) //极角相同的点,需要精确的比较函数语句,这里暂时
{
return distance(p[0], p1) < distance(p[0], p2);
}
else
{
return temp > 0;
}
}
std::sort(p + 1, p + n, compare);
3.构造一个栈结构,把前三个点压入栈。并遍历剩下的点集合。
- 当发现点是左转时,继续把该点压入栈
- 当发现点右转时,需要从栈中抛出上一个点,继续计算,如果依旧是右转,则继续抛出。直到是左转则压入栈
// 这最好用vector而不用stack
// 因为要随机访问栈顶下面的一个元素
// 可以用数组来间接实现stack的功能
std::vector <Point> convexHull;
convexHull.push_back(p[0]);
convexHull.push_back(p[1]);
convexHull.push_back(p[2]);
for (int i = 3; i < n; ++i)
{
// 从栈里拿出两个点组成线段convexHull[top],convexHull[top-1],和当前第i个点进行分析判断;
// 看第i个点是否右转,
// 如果右转,则抛出栈顶元素
// 如果左转 则压栈
while (convexHull.size() >1 && cross_product(convexHull[convexHull.size() - 2], p[i], convexHull[convexHull.size()-1]) >= 0)
{
ch.pop_back();
}
convexHull.push_back(p[i]);
}
//convexHull就是最后输出结果