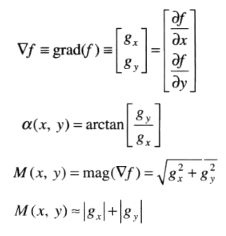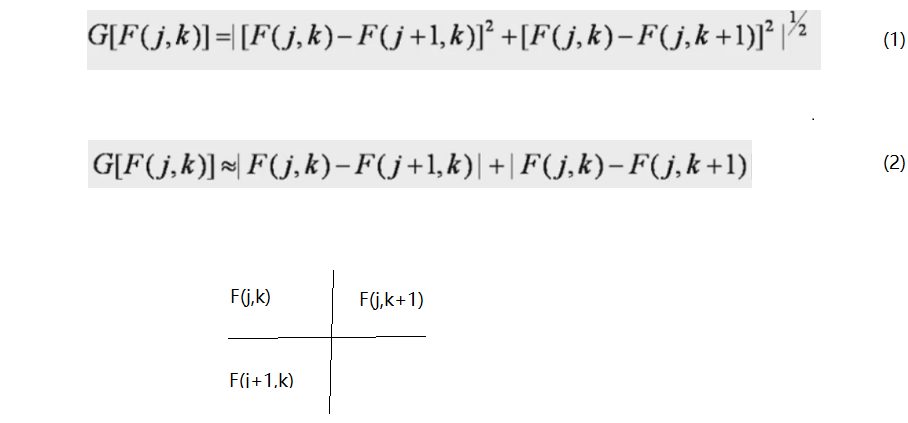本章主要介绍各种边缘检测的算法,通常边缘常用图像一阶导数和二阶导数来检测.
基于微分算子的边缘检测方法
原理介绍
一般常用一阶微分和二阶微分方法来检测边缘点:
- 在一阶微分图中极大值或极小值处是边缘;
- 在二阶微分图中极大值和极小值之间的过 0 点被认为是边缘;
梯度算子
梯度算子对应于图像的一阶导数,图像的一阶导数一般通过差分运算来近似的.
梯度的方向是图像最大变化率的方向,对图像F(j,k)在点(j,k)处的梯度定义为矢量:
对离散的图像,微分可以用差分来近似,如下图(1)式,便于编程和提高运算速度,在一些场合可以用绝对值表示,如下图二式,
利用幅值和方向可以进行假边缘点(非极大值)抑制: 遍历图像的每一个像素,假设某一像素P1,求出该像素的梯度值和梯度方向,在梯度方向上的前一个像素为p0 和后一下像素p2.并求出这两个像素的梯度值,如果P1的梯度值是三个像素的梯度的最大值,则是边缘点.否则,则不是,并将其梯度设为0.
关于梯度的介绍可以参见 另一篇总结《图像增强》
Prewitt算子
Roberts 交叉算子
另一篇总结《图像增强》
Sobel 算子
另一篇总结《图像增强》
Kirsch 算子
laplace 算子
另一篇总结《图像增强》
为了克服二阶微分对噪声敏感,可以用LOG算子,先进行图像平滑(高斯),然后再用拉普拉斯算子进行边缘检测.
Marr-Hidreth算子
laplace对噪声比较敏感,该算子的主要思路是首先对图像进行平滑处理然后再进行laplace算子.平滑函数常常选择Gauss函数.