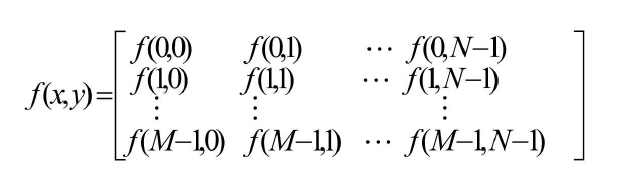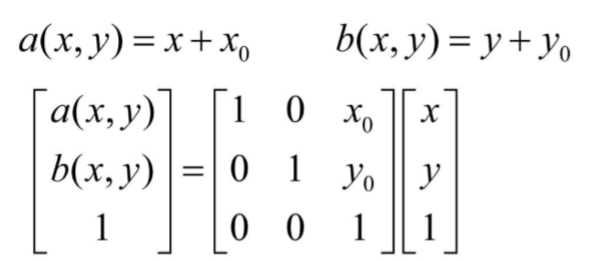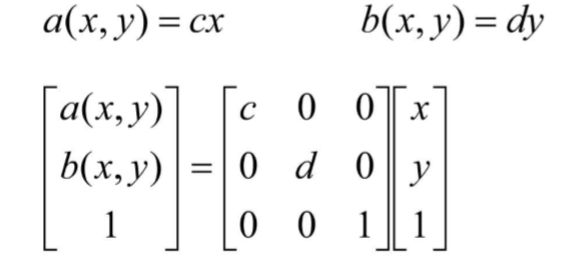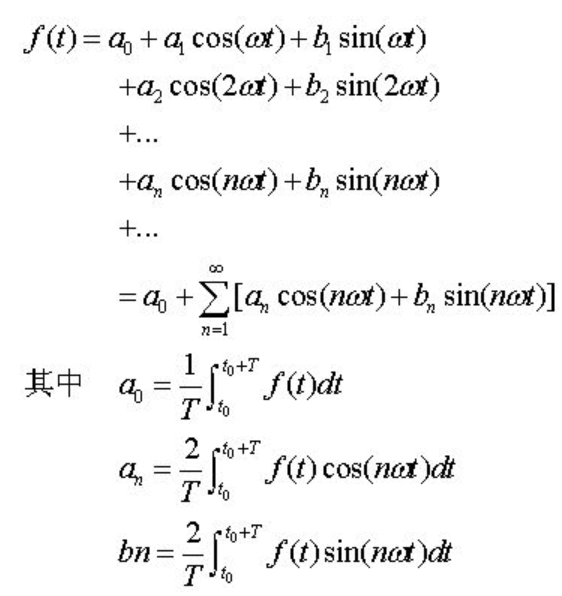本文主要总结数字图像的基本术语,以及数学变换.包括空间变换,傅立叶变换,以及灰度插值.
基本术语
- 图像(Image):图像是位图(Bitmap),它所包含的信息是用像素来度量的。对图像的描述与分辨率和色彩的种类数有关,分辨率与色彩位数越大,占用存储空间就越大,图像就越清晰。
-
图形(Graph):图形是矢量图(Vector Draw),它是根据几何特性来绘制的,图形的元素是一些点、直线、弧线等。图形任意放大或缩小后,依然非常清晰。矢量图常用于框架结构的形处理,应用非常广泛。
- 数字图像处理就是利用计算机对图形进行去噪,增强,复原,分割,提取,压缩,分析等理论方法和技术。
-
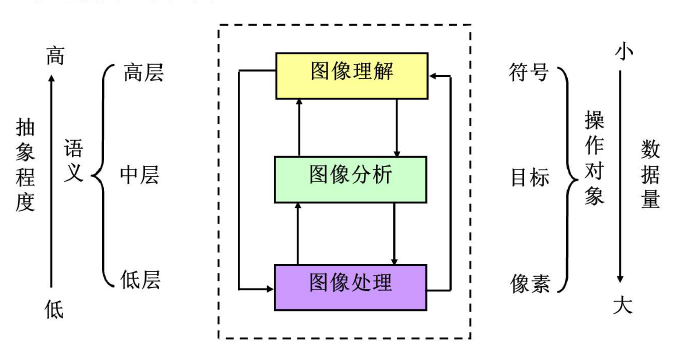
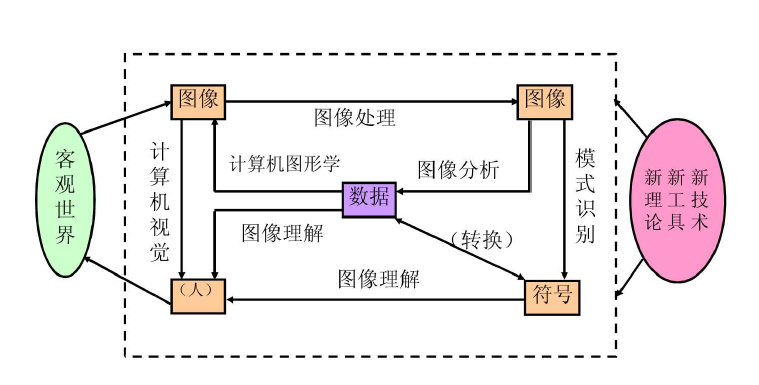
图像工程主要分为三层,且与其他的领域都有紧密的联系.
- 数字图像处理系统主要包括以下几个层面
- 通信
- 图像显示
- 图像存储
- 图像采集
- 图像处理及分析
- 颜色模型
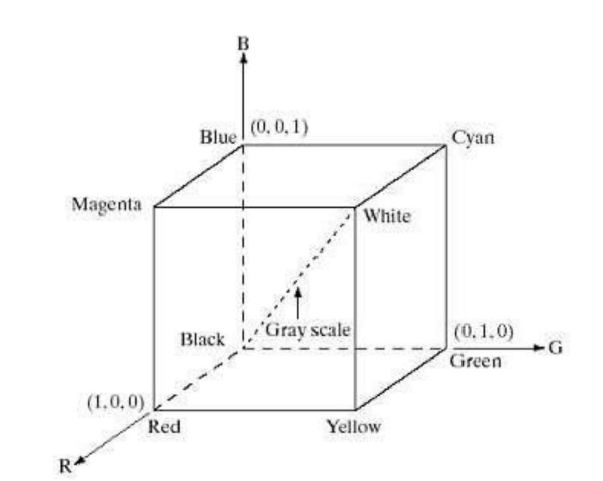
- RGB 模型
- CMY 模型 主要以品红(cyan),青magenta 黄yellow作为基色的颜色模型.
- HSI 模型
主要以色调hue,色饱和度saturation以及明度intensity.
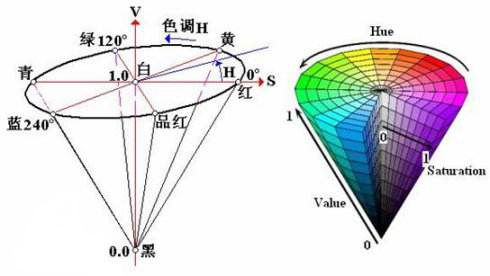
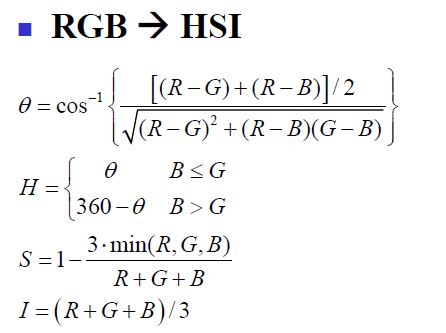
- RGB 模型
- 采样,量化:一般的图像(模拟图像)是不能直接用数字计算机来处理的,必须首先将各类图像转化为数字图像。采样就是把在时间上和空间上连续的图像转换为离散的采样点集的一种操作.
-
亮度:亮度是表示发光体(反光体)表面发光(反光)强弱的物理量。 人眼从一个方向上观察光源,在这个方向上的光强,与人眼所见到的光源面积之比,定义为该光源单位的亮度。
-
灰度:灰度使用黑色来显示物体,即黑色为基准色,不同饱和度的黑色来显示图像。通常,像素值量化后用一个字节(8B)来表示,如把有黑-灰-白连续变化的灰度值量化为256(2^8)个灰度级,灰度值的范围为0-255,表示亮度从深到浅,对应图像中的颜色为从黑到白。 换一种说法,即每个灰度对象都具有从0%(白色)到100%(黑色)的亮度值。 如果灰度范围为0-255,那么0是黑,255是白。
-
对比度:对比度是指一幅图像中最亮的白和最暗的黑之间不同亮度层级的测量,差异范围越大代表对比越大,差异范围越小代表对比越小。
- 饱和度:饱和度指色彩的纯洁性,叫饱和度或彩度,是“色彩三属性”之一。举个简单的例子,大红比玫红更红,这就是说大红的饱和度要更高。
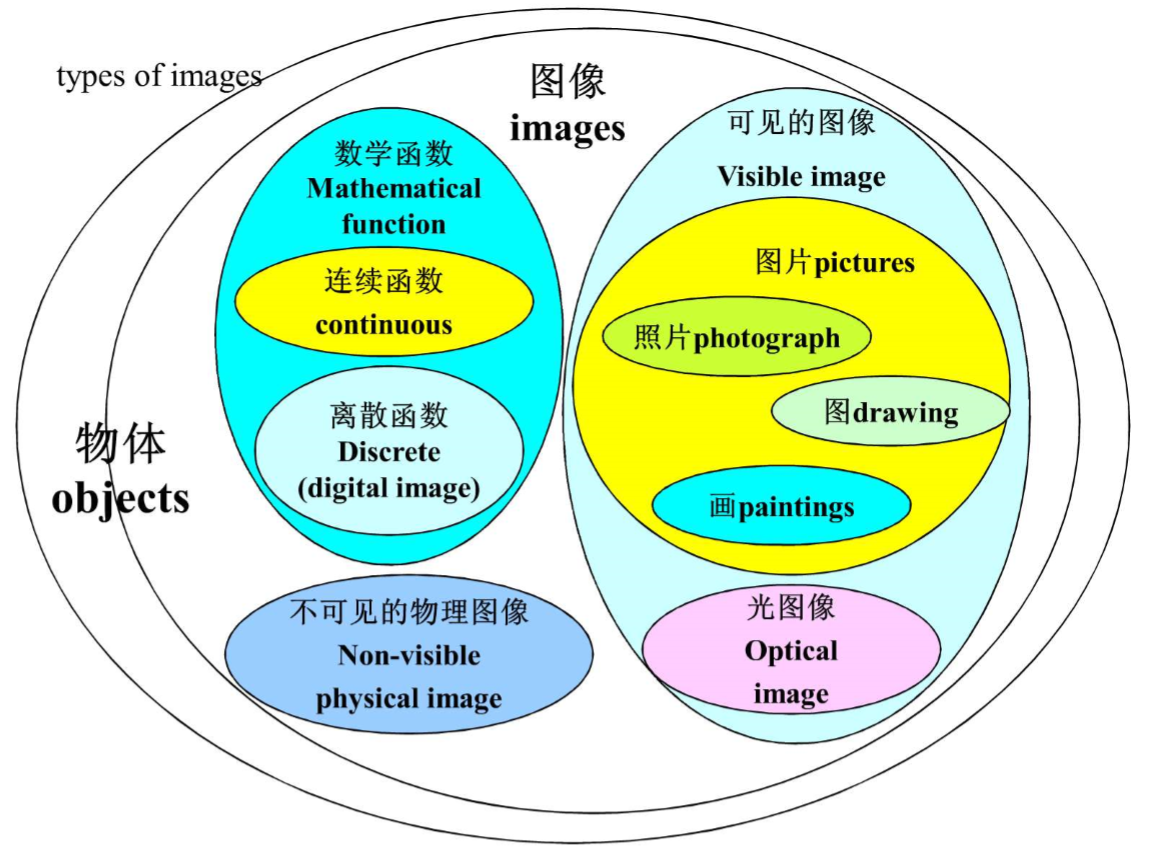
图像的表达
-
图像的分类
-
最普通的数学表达式 其中x,y,z是空间坐标,λ是波长,t是时间,I 是光强度
- 对待静态图像可以表达为 $ I = f(x,y) $
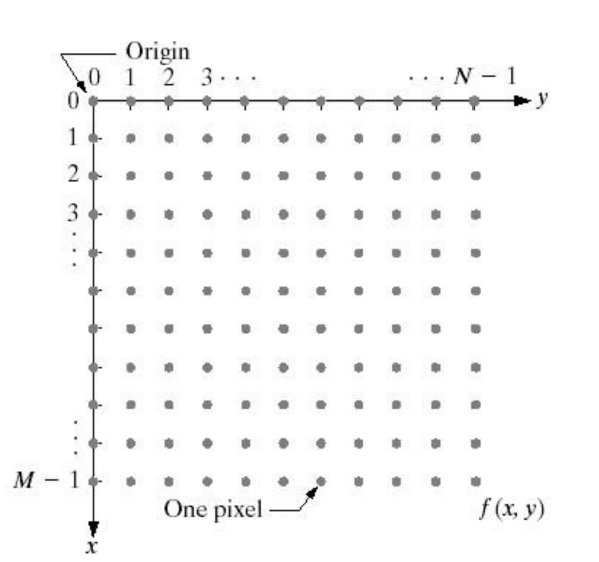
- 矩阵表示
图像像素的空间关系概念
- 相邻像素
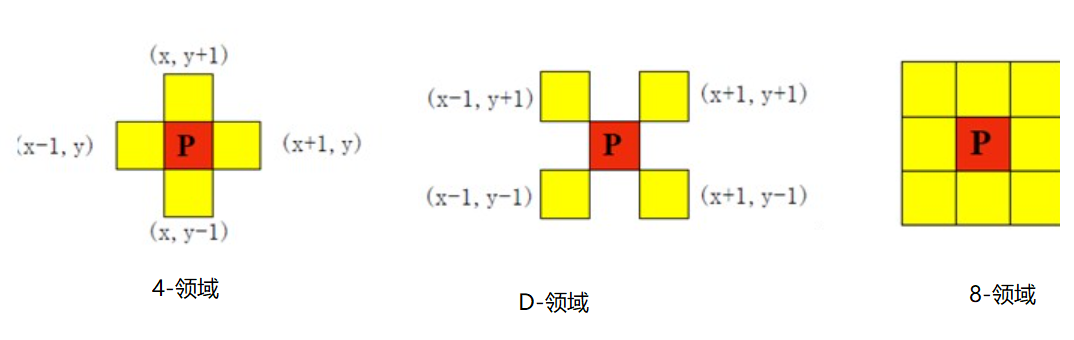
- 4领域:像素p(x,y)的4邻域是:(x+1,y);(x-1,y);(x,y+1);(x,y-1) 用N4(p)表示像素p的4邻域.
- D领域:像素p(x,y)的4邻域是: (x+1,y);(x-1,y);(x,y+1);(x,y-1) 用N4(p)表示像素p的4邻域
- 8领域:像素p(x,y)的8邻域是:4邻域的点+ D邻域的点
用N8(p)表示像素p的8邻域。 N8(p) = N4(p) + ND(p)
- 领接性
- v是定义领接性的灰度值集合,在二值图像中,如果具有1值得归属为领接像素,v={1};
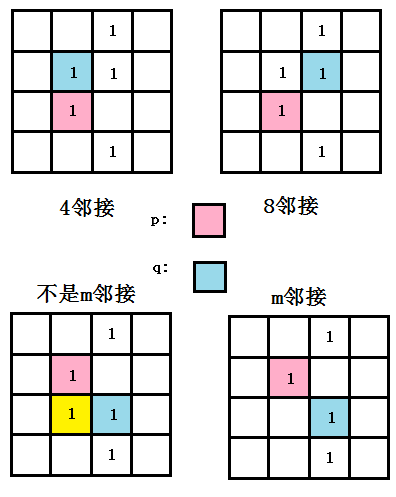
- 4-领接:如果像素q在集合N_4 (p)中,则具有V中灰度值的两个像素q和p是4邻接的。
- 8-领接:如果像素q在集合N_8 (p)中,则具有V中灰度值的两个像素q和p是8邻接的。
- m-领接:如果(1)q在集合N_4 (p)中,或者(2) 像素q在集合N_D (p)中,且集合N_4 (p)∩N_4 (q)没有来自V中灰度值的像素,则具有V中数值的两个像素p和q是m邻接的。
- 连通性
- 从坐标(x,y)的像素p到坐标为(s,t)的像素q的通路,是由一系列的特定像素组成的序列,其坐标为:(x0,y0), (x1,y1), …, (xn,yn) 其中(x0,y0) = (x,y), (xn,yn) = (s,t). 并且像素(xi,yi)和(xi-1,yi-1)对于1≤i≤n是邻接的(4邻接,8邻接,m邻接)。在这种情况下,n是通路的长度。从像素p到像素q就形成了一个像素通路.
- 若从p到q有一条通路,则称他们相连通.
- 距离量度
- 如果有两个像素点p(x,y) 和q(s,t);
- 欧式距离:$[(x-s)^2+(y-t)^2]^{1/2}$
-
城市距离:$ x-s + y-t $ -
棋盘距离:$max( x-s , y-t )$
数学变换
图像的像素级运算
点运算:线性和非线性点运算
- 线性:$ I(x,y) = a Input(x,y) + b $
- a <0:黑白反转
-
a >1: 增加对比度 -
a <1: 减少对比度 - b>0 增加量度
- b<0 减少量度
- 非线性:
代数变换:加减乘除
- 加法运算
二次曝光: $C(x,y) = aA(x,y)+bB(x,y)) 其中a+b=1 $ -
减法运算 (差分)
- 乘法运算: 一般用二值蒙版图像与原图做乘法,可以图像的局部显示
逻辑运算:求反,异或,或,与
- 图像反转: 如果灰度级范围为[0,L-1],则 反转图像后为 s = L-1-r;
图像的空域变换
空间域变换都可以用表达式 $g(x,y) = T[f(x,y)]$,其中T是变换算子.
几何变换
- 平移
- 旋转
图像旋转需要注意的是避免空洞点的产生,应该三角函数都是小数,运算过程会有误差产生. 需要重采样
- 镜像
- 放缩
- 灰度插值-重采样
在图像缩放,旋转等一些图像处理中,对图像进行插值是不可缺少的一个步骤,对失真图像进行几何校正,首先建立几何校正的数学模型,其次利用已经确定的模型参数,最后根据模型对图像进行几何校正;
主要分为两步:
- 图像空间的坐标变换。
- 确定校正空间各限速的灰度值.
输出像素通常被映射到输入图像中的非整数位置,即位于四个输入像素之间,因此,为了决定与该位置相对应的灰度值,必须进行插值运算,常用的插值方法有三种:
- 最近领插值 选择离它所映射到的位置最近的输入像素的灰度值为插值结果. 图像有马赛克的效果.
- 双线性插值
双线性插值又称为一阶插值,它是线性插值扩展到二维的一种应用,将周围四个点的像素值进行处理而作为该点的值,
其实就是领近四个点的加权平均值,也造成了边缘模糊.
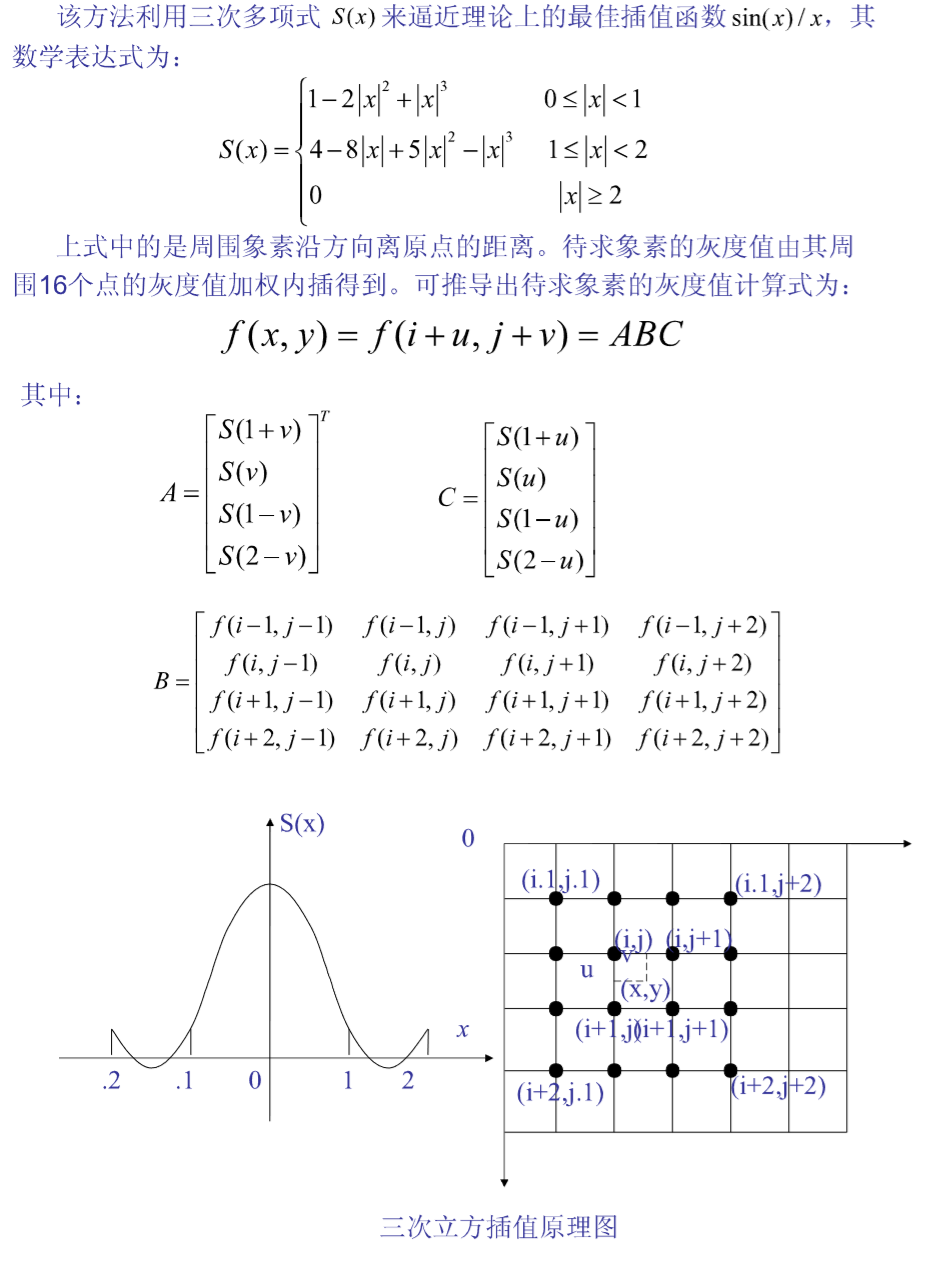
- 三次立方插值(高阶插值)
高阶插值是主要考虑周围有限个点,
非几何变换
- 模板运算
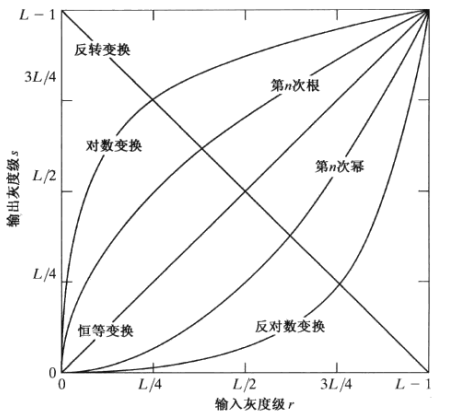
- 灰度变换
- 对数变换
- 伽马变换
-
分段线性变换
- 灰度级变换示意图
- 直方图变换
频域上的变换(傅立叶变换)
傅立叶级数
- 三角函数信号: w _0t+φ 是相位,
- 任何周期信号都能够由不同谐波的正弦波叠加而成,这由傅里叶发现,因此称之为傅里叶级数.
- 傅里叶级数的物理含义就是 任何时域连续的复杂波形,通过傅立叶变换都可以变成一系列简谐波之和.
- 傅立叶变换是全局性的,没法确定时间与空间位置
傅立叶积分
傅里叶变换
傅里叶认为,既然周期信号可以用正弦信号来表示,那么非周期信号也可以用正弦信号来逼近。原因是非周期信号可以看成是周期无限大的周期信号;事实证明,傅里叶的想法是对的,于是才有了大名鼎鼎的傅里叶变换

离散傅里叶变换
傅里叶变换的性质
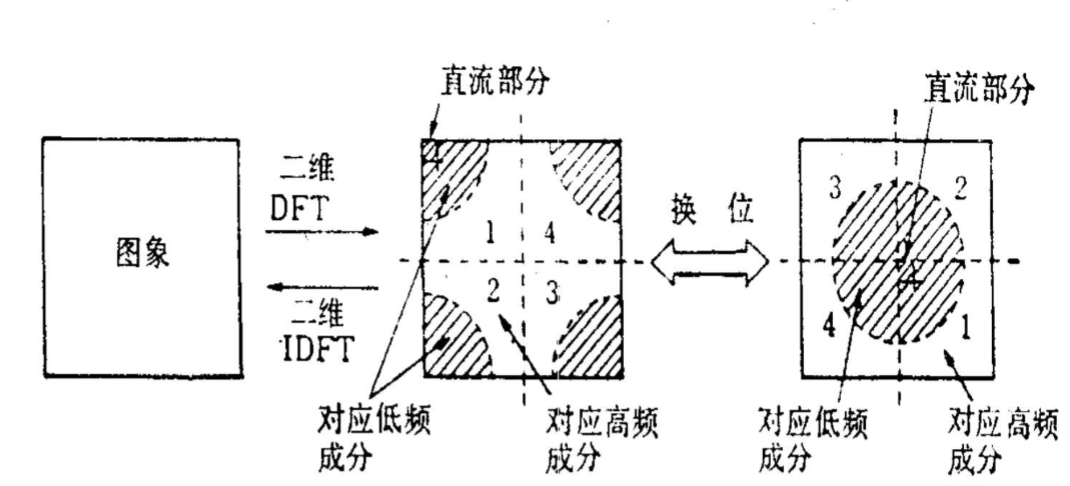
- 可分离性:也就是说一个二维傅立叶变换可以分解为两步进行,
每一步都是一个一维傅里叶变换.先对f(x,y)按行进行傅里叶变换得到F(x,v),在对F(x,v)按列进行傅里叶变换得到F(u,v),先列后行也是可以的.
。 回到图像的像素级别的话:每一行由N个像素点,对每一行的一维N点序列进行离散傅里叶变换得到F(x,u),再对得到F(x,u)按列向对每一列做M点的离散傅里叶变换,就可以得到二维图像f(x,y)的离散傅里叶变换F(u,v).
-
平移性
- 线性 F[af(x,y)+bg(x,y)] = aF(f(x,y))+bF(g(x,y));时域上的线性相叠加等于频域相加.
- 周期性
- 共轭对称性
- 旋转性
- 比例变换性
- Parseval 定理
- 相关定理
- 卷积定理
快速傅里叶变换
- 快速傅里叶变换 (fast Fourier transform),即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT
- 这里仅仅列出概念,需要特别的篇幅来所傅里叶
- 可以查看引用的两篇文章,或者《算法导论》,第四版,第30章 多项式与快速傅里叶变换.
离散傅立叶变换的显示
小波变换
Reference
- https://blog.csdn.net/enjoy_pascal/article/details/81478582
- https://blog.csdn.net/little_cats/article/details/81039747
- http://fourier.eng.hmc.edu/e161/lectures/