本文主要对空间矩阵变换的总结,其包括齐次坐标系,平移,旋转和缩放矩阵,仿射变换,以及用于计算机图形学中透视投影矩阵以及正交投影 的矩阵推导.
齐次坐标系
概念及其由来
In Euclidean space (geometry), two parallel lines on the same plane cannot intersect, or cannot meet each other forever. It is a common sense that everyone is familiar with.
However, it is not true any more in projective space(透视空间), for example, the train railroad on the side picture becomes narrower while it moves far away from eyes. Finally, the two parallel rails meet at the horizon, which is a point at infinity.

Euclidean space (or Cartesian space) describe our 2D/3D geometry so well, but they are not sufficient to handle the projective space (Actually, Euclidean geometry is a subset of projective geometry). The Cartesian coordinates of a 2D point can be expressed as (x, y).
What if this point goes far away to infinity? The point at infinity would be (∞,∞), and it becomes meaningless in Euclidean space. The parallel lines should meet at infinity in projective space, but cannot do in Euclidean space. Mathematicians have discoverd a way to solve this issue.Homogeneous coordinates, introduced by August Ferdinand Möbius, make calculations of graphics and geometry possible in projective space. Homogeneous coordinates are a way of representing N-dimensional coordinates with N+1 numbers.
Consider the following linear system in Euclidean space; And we know that there is no solution for above equations because of C ≠ D. If C = D, then two lines are identical (overlapped).
Let’s rewrite the equations for projective space by replacing x and y to x/w, y/w respectively.
Now, we have a solution, (x, y, 0) since (C - D)w = 0, ∴ w = 0. Therefore, two parallel lines meet at (x, y, 0), which is the point at infinity. Homogeneous coordinates are very useful and fundamental concept in computer graphics,such as projecting a 3D scene onto a 2D plane.
好处有哪些
- 齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换.
- 在计算机图形学中的几何变换,主要包括平移、旋转、缩放。以矩阵表达式来计算这些变换时,平移是矩阵相加,旋转和缩放则是矩阵相乘, 综合起来可以表示为 其中R旋转缩放矩阵, T为平移矩阵, input ,output为变换后的向量)。引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法,它提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法(当维数不同无法相乘时变换维数使其相乘)。
- 向量的最后一维通常为0,点的最后一维通常是值,如果点的最后一维度为0,则表示无穷远处。
仿射变换(Affine Transformation)
- Affine Transformation是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直性”(译注:straightness,即变换后直线还是直线不会打弯,圆弧还是圆弧)和“平行性”(译注:parallelness,其实是指保二维图形间的相对位置关系不变,平行线还是平行线,相交直线的交角不变。)
- 缩放(Scale)、平移(transform)、旋转(rotate)、反射(reflection)、错切(shear mapping,或者它们的任意组合
- 数学定义, 一个集合X的仿射变换模型为
-
An affine transformation preserves:
- collinearity between points: three or more points which lie on the same line (called collinear points) continue to be collinear after the transformation.
- parallelism: two or more lines which are parallel, continue to be parallel after the transformation.
- convexity of sets: a convex set continues to be convex after the transformation. Moreover, the extreme points of the original set are mapped to the extreme points of the transformed set.[3]
- ratios of lengths along a line:
- barycenters of weighted collections of points.
-
example:2D affine transformation matrix
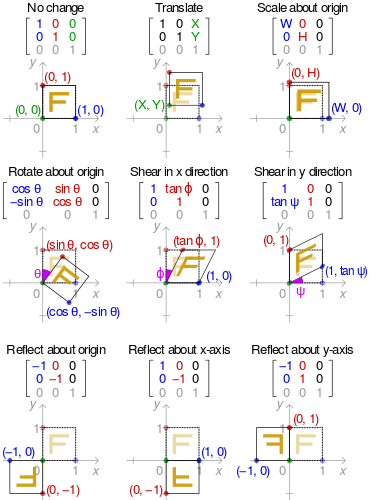
- 从仿射变换变换中看齐次坐标的好处
假设2维平面上一点 经过旋转和平移后的仿射变换可以写成:

旋转矩阵
平移矩阵
放缩矩阵
正交投影
从矩形视体到标准视体的转换;一旦你的顶点坐标已经在顶点着色器中处理过,它们就应该是标准化设备坐标了,标准化设备坐标是一个x、y和z值在-1.0到1.0的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪,不会显示在你的屏幕上。下面你会看到我们定义的在标准化设备坐标中的三角形(忽略z轴):
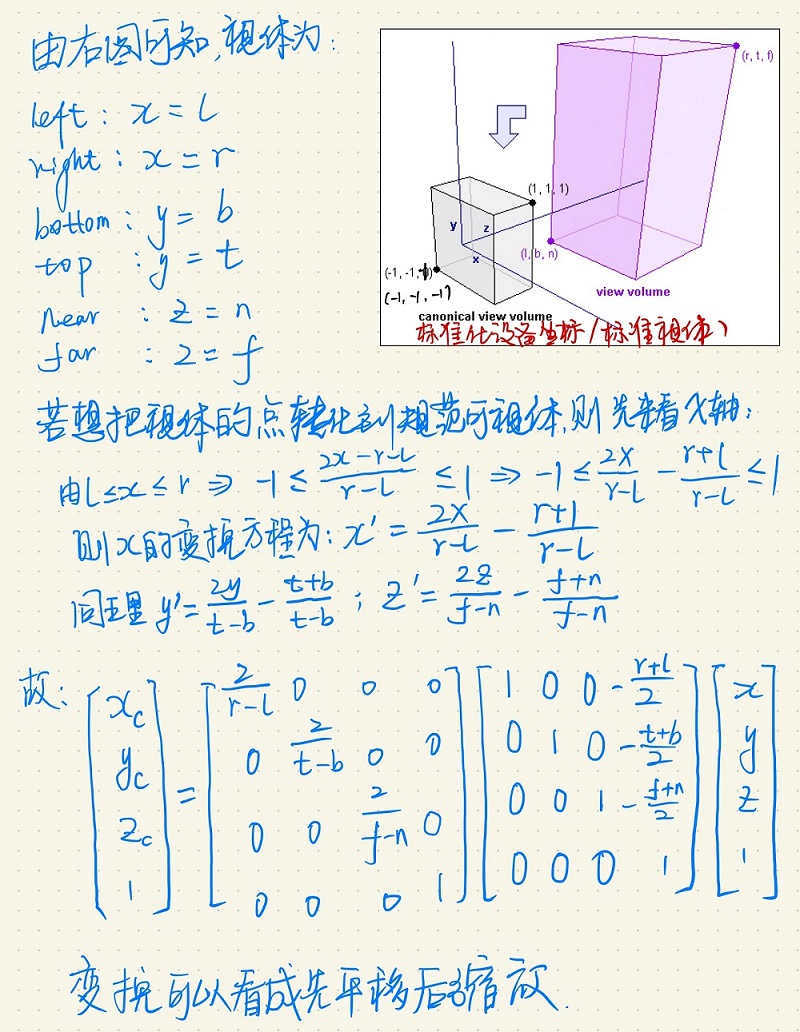
透视变换


Reference
- http://www.songho.ca/math/homogeneous/homogeneous.html
- https://en.wikipedia.org/wiki/Affine_transformation
- https://www.codeguru.com/cpp/misc/misc/graphics/article.php/c10123/Deriving-Projection-Matrices.htm#page-3
- https://learnopengl-cn.readthedocs.io/zh/latest/01%20Getting%20started/04%20Hello%20Triangle/



